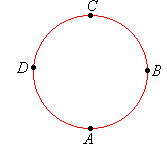
| Points that lie on the same circle are said to be concyclic.
For example, A, B, C and D are concyclic
points.
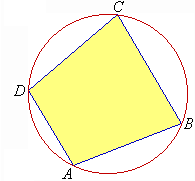
Cyclic Quadrilaterals
If the vertices of a quadrilateral lie on a circle, then the
quadrilateral is said to be cyclic. For example, ABCD is a cyclic quadrilateral since the vertices A, B, C and D lie on the circle.
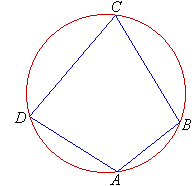
Theorem
Use the information given in the diagram to prove that the opposite
angles of a cyclic quadrilateral are supplementary.
That is:
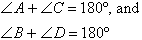
Given:
A cyclic quadrilateral ABCD.
To prove:
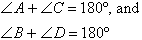
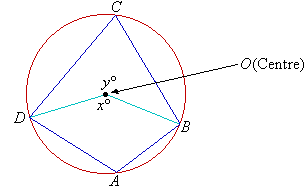
Construction:
Let O be the centre of the circle. Join O to B and D. Then let the angle subtended by the minor arc and the
major arc at the centre be xº and yº respectively.
Proof:


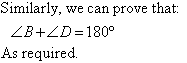
In general:
Opposite angles of a cyclic quadrilateral are supplementary.
Example 28
Find the value of each of the pronumerals in the following diagram.
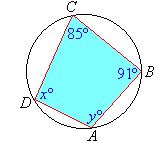
Solution:

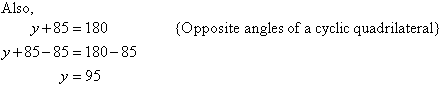
Example 29
Find the value of each of the pronumerals in the following diagram.
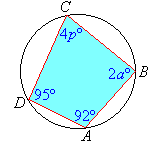
Solution:
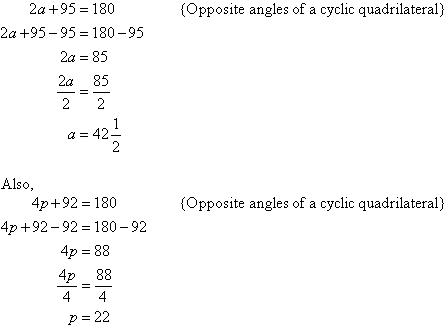
Exterior Angle of a Cyclic Quadrilateral
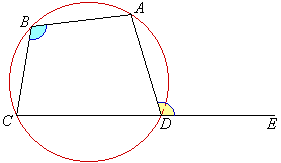
Theorem
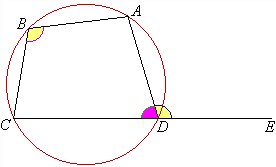
Use the information given in the diagram to prove that the exterior
angle of a cyclic quadrilateral is equal to the interior opposite angle.
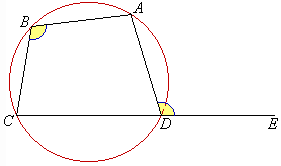
That is:
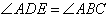
Given:
A cyclic quadrilateral ABCD with side CD extended to E.
To prove:
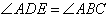
Proof:
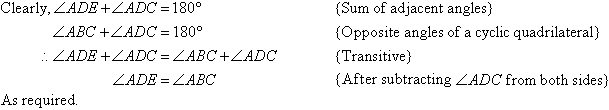
In general:
The exterior angle of a cyclic quadrilateral is equal to the interior
opposite angle.
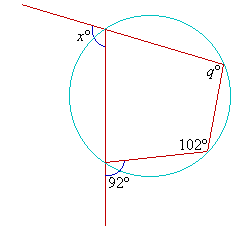
Example 30
Find the value of each of the pronumerals in the following diagram.
Solution:
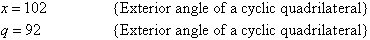
Example 31
Find the value of each of the pronumerals in the following diagram.
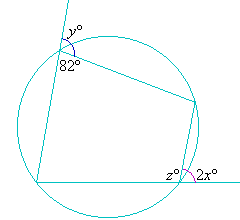
Solution:

Key Terms
concyclic points, cyclic quadrilateral, opposite angles of a cyclic quadrilateral, exterior
angle of a cyclic quadrilateral |