Year 10 Interactive Maths - Second Edition

Pythagoras' Theorem

Pythagoras' Theorem states that:

In any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. That is:

Proof of Pythagoras' Theorem

Cut out four congruent right-angled triangles. Place them as shown in the following diagram.

The figure ABCD is a square with side length a + b, and it consists of the four congruent right-angled triangles and a square, EFGH, with side length c.

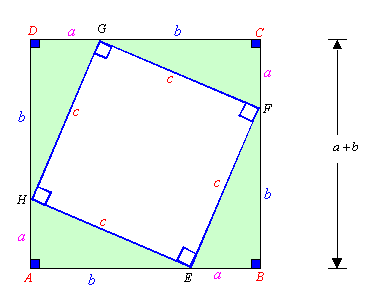
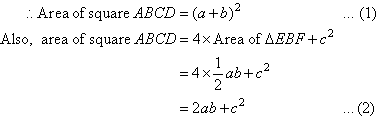
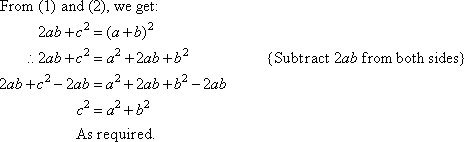
This proof was devised by the Indian mathematician, Bhaskara, in 1150 AD.

Applications of Pythagoras' Theorem

To solve a word problem, read the problem and draw a diagram. Then write the given information on the diagram and identify any right-angled triangle(s).  Use Pythagoras' Theorem to form an equation and solve the equation thus obtained.  Translate the solution into a worded answer.

Example 1

A ship sails 80 km due east and then 18 km due north. How far is the ship from its starting position when it completes this voyage?

Solution:

Let the distance of the ship from its starting point be x km. We can draw a diagram of the ship's voyage on a set of axes, with the horizontal axis representing east and the vertical axis representing north. The ship is at the point P and it started at the origin. There is a right angle at A.

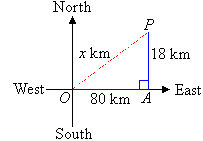
By Pythagoras' Theorem from triangle OAP,

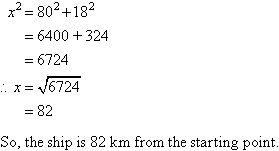
Example 2

A ladder 7.25 m long stands on level ground so that the top end of the ladder just reaches the top of a wall 5 m high. How far is the foot of the ladder from the wall?

Solution:

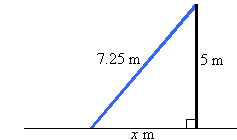
Let the distance from the foot of the ladder to the base of the wall be x m.
By Pythagoras' Theorem and the diagram,

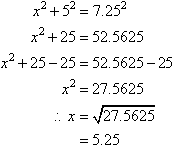
So, the distance from the foot of the ladder to the wall is 5.25 m.

Using a Construction Line

Sometimes we need to draw a construction line (shown as a broken line) in the diagram to form a right-angled triangle.

Example 3

Use the information given in the following diagram to find the value of x.

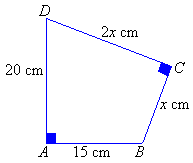
Solution:

Join BD by a broken line to form the right-angled triangles ABD and BCD.  Let BD = y cm.

Pythagoras' Theorem in Three Dimensions

A three-dimensional object can be described by three measurements - length, width and height.

We can use Pythagoras' Theorem to find the length of the longest straw that will fit inside the box or cylinder.

Example 4

A can of drink is in the shape of a cylinder with height 15 cm and radius 4 cm.  What is the length of the longest straw that will fit inside the can?

Solution:

Let the length of the straw be x cm.

So, the length of the longest straw that will fit inside the can is 17 cm.

Key Terms

Pythagoras' Theorem, hypotenuse, construction line