A table helps us to organise and analyse a set of data values. In this
section we will consider frequency tables and stemplots (i.e.
stem-and-leaf plots).
Frequency Tables
A frequency table is a tabular representation of a data set in
an ascending order of magnitude with their corresponding frequencies. It
is a simple device to provide a count of how often a data value occurs.
Note:
The word 'frequency' means 'how often'.
Example 7
The scores awarded to 25 students for an assignment were as follows:
4 7
5 9
8 6
7 7
8 5
6 9 8
5 8
7 4
7 3
6 8
9 7
6 9
Present this information in a frequency table and find the mode.
Solution:
The frequency table is as follows:
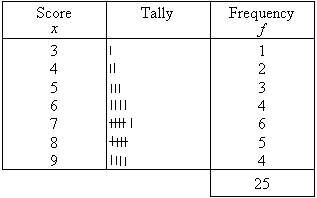
The score that occurs most often is 7.
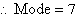
Class Intervals
The data is grouped into class intervals if the frequency table becomes
too large to help us organise, interpret and analyse the data. The
frequency of a class interval is the number of data values that fall in
the range specified by the interval.
The size of the class interval is often selected as 5, 10, 15 or 20
etc. Each class interval starts at a value that is a multiple of the size.
For example, if the size of the class interval is 5, then the class
intervals should start at 0, 5, 10, 15, 20 etc. The class intervals will
then be 0-4, 5-9, 10-14 etc.
Frequency Tables with Class Intervals
A frequency table for a data set containing a large number of data
values is constructed as follows:
- Determine the data range of the data set.
- Decide the width of the class intervals.
- Divide the range by the chosen width of the class interval to
determine the number of intervals.
Example 8
A school nurse weighed 30 students in Year 10. Their weights (in kg)
were recorded as follows:
50 52
53 54
55 65
60 70
48 63
74 40
46 59
68 44
47 56
49 58
63 66
68 61
57 58
62 52
56 58
a. Present this information in a frequency table.
b. Comment on the mode of the table.
Solution:
a.
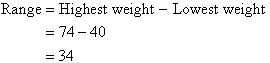
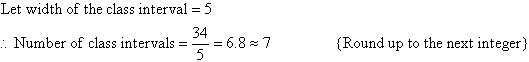
There are 7 class intervals. This is reasonable for the given data.
The frequency table is as follows:
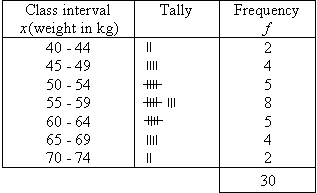
b.
We notice that the modal class interval is 55-59. That is, most of the
students weigh between 55 and 59 kilograms.
Stemplots (Stem-and-leaf Plots)
A stemplot (stem-and-leaf plot) is a device used to group a
small data set (up to about 50 data values). The data set is arranged in
ascending order while retaining all the original data values. This enables
us to find the first
quartile, median and the third quartile readily. The
stemplot is useful to obtain information about the centre, spread, shape
and outliers of the distribution.
Constructing a Stemplot
In a stemplot, each data value is considered to have two parts, a stem and a leaf. The leading digit(s) of a data value form the stem, and
the trailing digit(s) becomes the leaf.
Three examples of a stemplot follow:
- Data values 65, 70 and 74 are recorded as shown below:


- Data values 349, 366 and 480 are recorded as shown below:


- Data values 35.8, 36.2 and 36.9 are recorded as shown below:


Note:
To construct a stemplot, we:
- enter the stems to the left of a vertical dividing line and the leaf to the right of the vertical dividing line for each data value
- record each data value as listed in the data set to construct an
unordered stemplot.
- Then we construct an ordered stemplot from the unordered version by
arranging the leaves in ascending order.
Example 9
Prepare a stemplot for the following set of scores which are marks
obtained by 16 students:
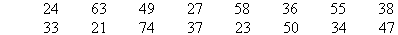
Solution:
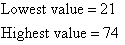
A stemplot for the score values that range from 21 to 74 is as follows:

This stemplot is not ordered.
An ordered stemplot is obtained by arranging the leaves in order, as
shown below.

Note:
For each value of the data, the stem is the tens digit and the leaf is the units digit.
Example 10
The following data represents the number of runs per innings a player
has scored in a season.
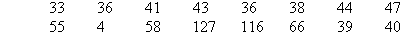
Construct an ordered stemplot to display the data.
Solution:
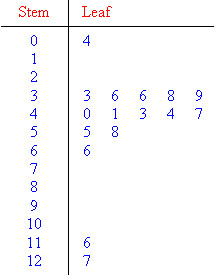
An ordered stemplot for the scores that range from 4 to 127 is given
below. Stems 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are formed by the tens
digits; whereas, the stems 10, 11 and 12 are formed by the hundreds and
tens digits. The leaves are formed by the unit digits of the values.
We notice that the scores 4, 116 and 127 are separated from the main
body of the data. So, 4, 116 and 127 are outliers. The stemplot for
the data consisting of outliers can be displayed as follows:
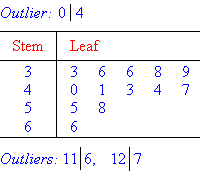
Note:
The value of 4 is listed at the top of the table as an outlier and the
values of 116 and 127 are listed below the table as outliers.
Key Terms
tables, frequency tables, class
intervals, stemplots, stem-and-leaf
plots, stem, leaf |