Fashion designers, builders, architects and engineers use accurate
constructions (or diagrams) to communicate their ideas to others. In
this section, we will consider some of the basic constructions used in
geometry.
Constructing Triangles
If the measurements of three sides, the measurements of two sides and the
angle between them, or the measurements of two angles and the side between
them are given, then a triangle can be constructed by using a ruler,
protractor and compass.
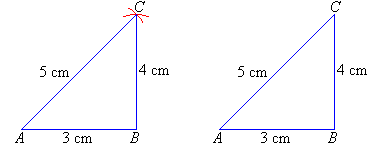
Constructing a Triangle given Three Sides
Example 13
Using a ruler and compass, construct a triangle ABC with AB = 3 cm, BC = 4 cm and AC = 5 cm.
Solution:
Step 1: Draw a line, AB, 3 cm long.
Step 2: Draw an arc of radius 4 cm with B as the centre.
Step 3: Draw an arc of radius 5 cm with A as the centre
to cut the arc drawn in Step 2 at C.
Step 4: Join, C, the point of intersection of the two
arcs to the points A and B.
Step 5: Erase the arcs to obtain the required triangle ABC.
Constructing a Triangle given Two Angles and the Side between them
Example 14
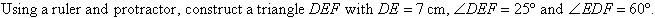
Solution:

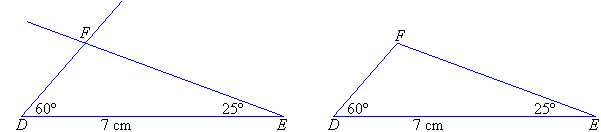
Constructing a Triangle given Two Sides and an Angle
Example 15
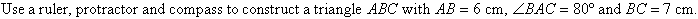
Solution:

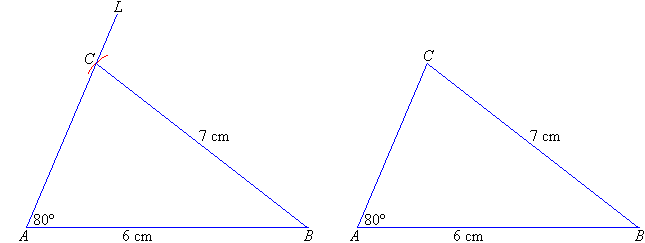
Constructing a Triangle given Two Sides and the Angle between them
Example 16
Solution:
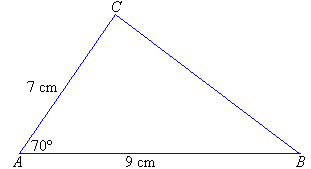
Step 1: Draw a line, AB, 9 cm long.
Step 2: Mark an angle of 70º by placing the centre of the
protractor at the point A.
Step 3: Join the 70º mark and the point A. Extend the
arm AC until it is 7 cm long.
Step 4: Join the points B and C to obtain the
required triangle ABC.
Activity 10.4

Key Terms
constructions, constructing
triangles |