Plane figures and solids can be changed (or transformed) by translation, reflection and dilation. The symmetry of shapes is related to translation,
reflection and rotation.
Reflection
Triangle ABC and its reflection A'B'C' have the same size and shape, that is they are congruent.
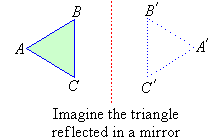
Translation
A translation is defined by specifying the distance and the
direction of a movement. For example, triangle ABC is translated by 2
units to the right.
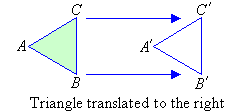
Triangle ABC and its image A'B'C' have the same size and shape. That is, they are congruent.
Rotation
Rotation is defined by stating the centre of rotation, amount of
turning in degrees and the direction of rotation (clockwise or
anticlockwise). For example, triangle ABC is rotated about O through 90º in an anticlockwise direction.
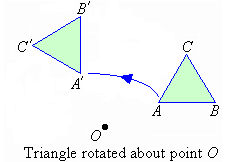
Triangle ABC and its image A'B'C' have the same size and shape, that is they are congruent.
We notice that:
The reflection, translation and rotation are congruent transformations.
Dilation
If a figure is enlarged or reduced and retains its shape, then it is said
to be dilated. This is an aspect of similarity as shown below.
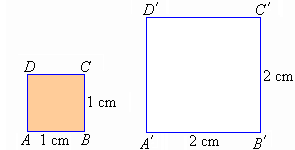
Note that the stretching (or shrinking) of a shape is called a dilation.
It is clear that dilation is not a congruent transformation, because the
size of the shape is changed.
In general:
- Lengths and areas are not preserved under dilation.
- If the dilation factor is the same for each side of the figure, then
the figures are similar.
Key Terms
transformation, reflection, translation, rotation, centre
of rotation, amount of turning, direction
of rotation, dilation, dilated, similarity |