Probability is an interesting branch of mathematics that is widely
used in genetics, insurance, finance, medicine, sociological surveys,
marketing and science. We use probability to measure the chance or likelihood of an event or events occurring in the future.
Events
An event is something that may or may not occur at some time or
during some period in the future.
When we talk about events in terms of chances, we could make statements
such as:
"I will probably play tennis this summer"
"It isn't likely that I will be invited to play in the
Australian Open Tennis Tournament"
"My chances of winning Tattslotto are not very good"
We could describe the expected occurrence of an event (or events) with
the words certain, probable, fifty-fifty, improbable and impossible.
These words tell us something about whether or not the event is expected to
occur; but the statements are very vague. We study and apply
probability to enable us to better quantify or measure the chance of an
event (or events) occurring in the future.
The Probability Scale
If an event is impossible, its probability is 0. If an event
is certain to occur, its probability is 1. The probability of
any other event is between these two values. That is:
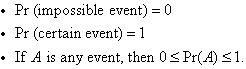

Probability Experiment
A probability experiment involves performing a number of trials to enable us to measure the chance of an event occurring in the
future. A trial is a process by which an outcome is
noted.
For example, consider the following three experiments:
Experiment: Roll a die two
hundred times noting the outcomes.
Event of interest: A six faces
upwards.
Trial: Roll the die once.
Number of trials: 200
Outcomes: 1, 2, 3, 4, 5 or 6
Experiment: Toss a coin seventy
times noting the outcomes.
Event of interest: A tail faces
upwards.
Trial: Toss the coin once.
Number of trials: 70
Outcomes: Head or Tail
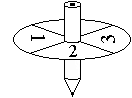
Experiment: Spin a spinner one
hundred times noting the outcomes.
Event of interest: The spinner
stops on the number 3.
Trial: Spin the spinner once.
Number of trials: 100
Outcomes: 1, 2, 3, 4
The Sample Space
The sample space of an experiment is the set of all possible outcomes of any trial of the experiment to be conducted.
For example, if an unbiased coin is tossed, then the two possible
outcomes are 'head' and 'tail'. The set of all possible outcomes is
therefore {H, T}. This is called the sample space of the
experiment and is denoted by S.
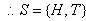
An element of the sample space is called a sample point.
For the example under consideration, the sample points are H and T.
Activity 16.1
To investigate the probability of obtaining a head (or tail) when a
coin is tossed.
Experiment - Toss the coin 100 times and complete the following
table.
| Outcome |
Tally of outcomes |
Total
number of trials in which the outcome occurred |
Tail
Head |
|
|
Sum |
|
If the coin is unbiased (i.e. well balanced), we say it is just as likely
to turn up heads as tails. In the activity under consideration, we would
expect about half of the coin tosses to turn up heads. Does this agree
with your result?

Long Run Proportion
Long run proportion is defined as the ratio of favourable outcomes to
the total number of trials in an experiment after conducting a very large
number of trials.

When we express the 50 chances of tossing a head (or tail) to the 100
coin tosses as a ratio, we are describing the chances of tossing a head (or
tail) in terms of a probability or long run proportion.
From the preceding discussion, we can conclude that:
The concept of long run proportion enables us to determine the
probability (or chance) of an event.
Key Terms
probability, chance, likelihood, event, probability scale, impossible, certain, probability experiment, trial, outcome, sample space, sample
point, long run proportion |