Axioms
An axiom is a statement that is simply accepted as being
true. We have accepted the following statements as facts:
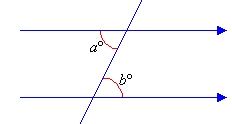
1. Alternate angles are equal. That is:
aº = bº
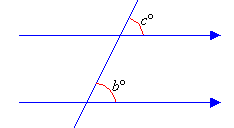
2. Corresponding angles are equal. That is:
bº = cº
3. The sum of adjacent angles forming a straight line is equal to 180º.
That is:
aº + bº = 180º

In deductive geometry, we do not accept any
other geometrical statement as being true unless it can be proved (or
deduced) from the axioms.
A statement that is proved by a sequence of logical steps is called a theorem.
To prove a theorem we start by using one or more of the axioms in a
particular situation to get some true statements. We then have to
apply logical reasoning to these statements to produce new statements that
are true. The proof ends when we arrive at the statement of the
theorem.
Properties of Equality
The relation of equality has the following properties. We will use
these properties in the proofs of some theorems.
1. Transitive Property
If a = b and b = c, then a = c.
2. Substitution Property
If a statement about a is true and a = b, then the
statement formed by replacing a with b (throughout) is also
true.
E.g. If the statement a + c = 180 is true and a is
equal to b, then the statement b + c = 180 is also
true.
Deductive Proofs of Theorems
To prove a theorem, draw a diagram. Write related statements and
give the reasons for each (i.e. state the axioms used). Then use the
transitive property and/or one of the other properties of equality.
Angle Sum of a Triangle
Theorem 1
Prove that the angle sum of a triangle is 180º.
Proof:
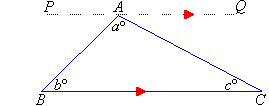
Consider any triangle ABC in which the
angles are aº, bº and cº. Draw a line
through A parallel to BC.

Further theorems can now be deduced by using this theorem together with
the axioms. This is how the body of knowledge is increased using the
deductive method.
The Exterior Angle of a Triangle
Theorem 2
Prove that the exterior angle of a triangle is equal to the sum of the
interior opposite angles.
Proof:
Consider any triangle ABC in which the angles are aº, bº
and cº. Extend the line BC to the point D.
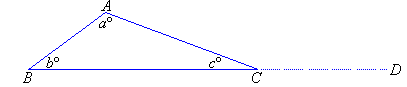

Hence the exterior angle of a triangle is equal to the sum of the
interior opposite angles.
Applying Properties of Angles in Triangles
The theorems we have proved can be used to prove other theorems.
They can also be used to find the values of the pronumerals in a problem.
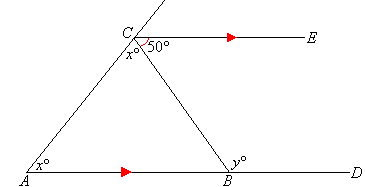
Example 12
Find the values of the pronumerals x and y in the
following diagram.
Solution:
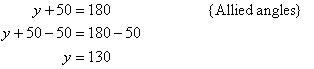

Key Terms
deductive geometry, axiom, theorem, equality, properties of
equality, transitive property, substitution
property, deductive proof of theorems, angle
sum of a triangle, exterior angle of a triangle |