| A population is the whole set of items from which a
data sample can be drawn; so a sample is only a portion of the
population data. Features of a sample are described by statistics.
Statistical methods enable us to arrange, analyse and interpret the
sample data obtained from a population. We gather sample data when
it is impractical to analyse the population data as a smaller sample often
allows us to gain a better understanding of the population without doing
too much work or wasting precious time.
Measures of Central Tendency
We make inferences about a population from a sample set of observed
values by finding the mean, median and mode. The mean, median and mode are collectively known as measures of central tendency.
Mean
The mean (or average) of a set of values is defined as the sum of all the
values divided by the number of values. That is:
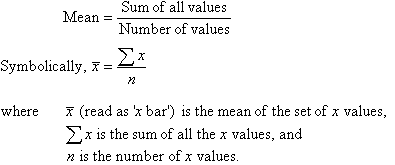
Example 1
The marks of five candidates in a mathematics test with a maximum
possible mark of 20 are given below:
14 12
18 17 13
Find the mean value.
Solution:
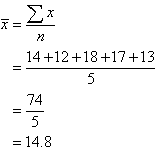
So, the mean mark is 14.8
Median
The median is the middle value of the data set
arranged in ascending order of magnitude.
E.g. the median of 3, 5 and 9 is 5 as it is the middle value.
Example 2
The marks of five candidates in a geography test for which the maximum
possible mark was 20 are given below:
18 17
15 14 19
Find the median mark.
Solution:
Arrange the marks in ascending order of magnitude:
14 15
17 18 19
The third value, 17, is the middle one in this arrangement.
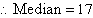
Note:
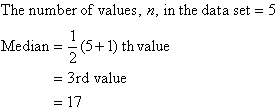
In general:

If the number of values in the data set is even, then the median is
the average of the two middle values.
Example 3
Find the median of the following scores:
10 16
14 19
8 11
Solution:
Arrange the values in ascending order of magnitude:
8 10
11 14
16 19
There are 6 values in the data set.
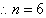
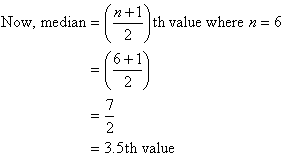
The third and fourth values, 11 and 14, are in the middle. That
is, there is no one middle value.
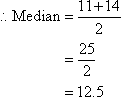
Note:
Half of the values in the data set lie below the median and half lie above the median.
Mode
The mode is the value (or values) that occurs most
often.
E.g. the mode of the data set {3, 5, 6, 7, 7, 7, 8, 8, 9} is 7 as it
occurs most often.
Example 4
The marks awarded to seven pupils for an assignment were as follows:
18 14
18 15
12 19 18
a. Find the median mark.
b. State the mode.
Solution:
a. Arrange the marks in ascending order of magnitude:
12 14
15 18
18 18 19
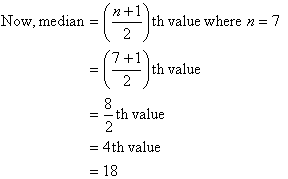
Note:
The fourth mark, 18, is the middle data value in this arrangement.
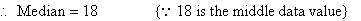
b. 18 is the mark that occurs most often.
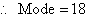
Note the following:
- The mode has applications in manufacturing. For example, it is
important to manufacture more of the most popular cars, because
manufacturing different cars in equal numbers would cause a shortage
of some cars and an oversupply of others.
- The mean (or average) of a set of data values is used to predict
future results.
- The median is easy to comprehend. Extreme values in the data
set do not affect the median.
Key Terms
statistics, population, sample, measures of central
tendency, mean, average, median, mode |