| In mathematics, we use symbols to denote relations and we build mathematical sentences using numbers, pronumerals and relations.
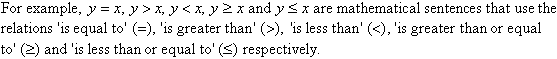
Consider the following sentence:
The cost (in dollars) of buying pens is equal to ten times the number
of pens bought.
If c represents the cost in dollars and p represents the
number of pens bought, then this sentence can be expressed mathematically
as
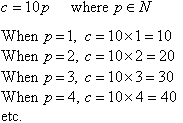

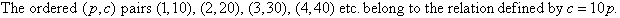
This suggests the following definition:
A relation is a set of ordered pairs, and is usually defined by
a rule.
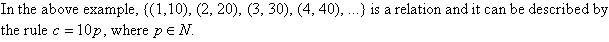
Domain
The domain of a relation is the set of all first elements
(usually x values) of its ordered pairs.
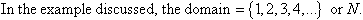
Range
The range of a relation is the set of all second elements
(usually y values) of its ordered pairs.

Note:
The graph of c against p is discrete because p is
an element of the set of natural numbers. The values of c depend
upon p. So, we say that p is an independent variable
and c is a dependent variable.
Example 1
State the domain and range of the following relations:
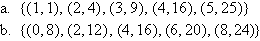
Solution:
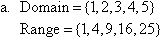
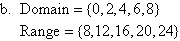
Functions
A relation is said to be a function if each element of
the domain determines exactly one element of the range.
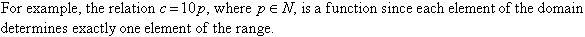
Domain of a Function
The domain of a function is the set of all first elements
(usually x values) of its ordered pairs.
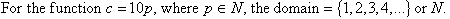
Range of a Function
The range of a function is the set of all second elements
(usually y values) of its ordered pairs.
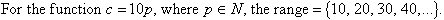
Example 2
State the domain and range of the following functions:
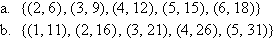
Solution:
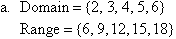

Key Terms
relations, mathematical sentences, domain, range, independent variable, dependent variable, function, domain of a function, range
of a function |