Year 10 Interactive Maths - Second Edition

Problem Solving Unit

Problem 4.1  The Numbers

What are D, E and F?

Problem 4.2  Finite Difference Table

Consider a finite difference table of the linear function y = 2x + 5.

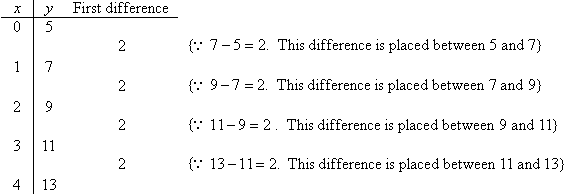
For the linear function y = 2x + 5, the first difference in a finite difference table is constant and it is equal to 2. This constant is the gradient of the linear function. When x = 0, y = 5. We can write this as y(0) = 5 which is the y-intercept.

Consider the finite difference table of the general linear function  y = mx + c where m is the gradient and c is the y-intercept.

Clearly, the first difference is the constant m; and it is the gradient of the linear function.
y-intercept = y(0) = c.

From this we can infer that:

If a finite difference table for a function generates a constant first difference, then it must be a linear function. Note that if the table also includes x = 0, it allows us to easily find a rule for the linear function.

Example 10

Find a rule for the function specified by the following table of values:

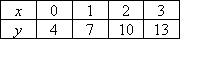
Solution:

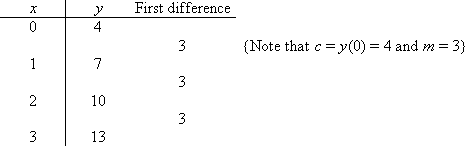
The first difference is constant.  Therefore, the table of values represents a linear function of the
form y = mx + c.

To find m and c, we compare this table with the finite difference table of y = mx + c.

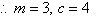
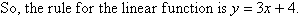
Note:

A table of values must include x = 0 as it helps to find the value of c

Using a TI-83 Graphics Calculator

Clear any list(s) within the STAT menu (and if there are graphs in memory clear them using the
Y = menu). Select EDIT from the STAT menu and enter x values under L₁ and y values under
L₂. Both lists should have the same number of entries.

Select Plot 1 on from the STAT PLOT menu and turn the other plots off. Highlight the second
plot that gives a line graph. Choose L₁ for the Xlist and L₂ for the Ylist (if they are not already
highlighted).

Choose Zoom Stat from the ZOOM menu to obtain the graph of the data, which is a straight
line. Then choose LinReg in the CALC section of the STAT menu. The screen display shows
that the relation

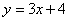
fits the data.

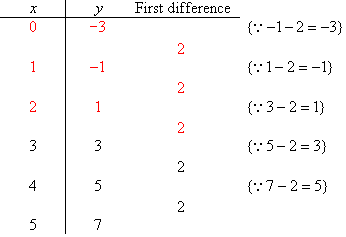
Example 11

Find a rule for the function specified by the following table of values:

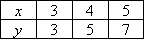
Solution:

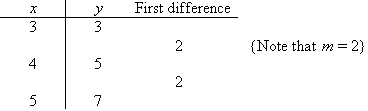
The first difference is constant.  Therefore, the table of values represents a linear function of gradient 2.  So, m = 2.  To find c = y(0) we extend the table as shown below.

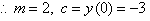
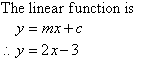
Using a TI-83 Graphics Calculator

Clear any lists within the STAT menu (and if there are graphs in memory, clear them using the
Y = menu). Select EDIT from the STAT menu and enter x values under L₁ and y values under
L₂. Both lists should have the same number of entries.

Select Plot 1 on from the STAT PLOT menu and turn the other plots off. Highlight the second
plot that gives a line graph. Choose L₁ for the Xlist and L₂ for the Ylist (if they are not already
highlighted).

Choose Zoom Stat from the ZOOM menu to obtain the graph of the data which is a straight line.
Then choose LinReg in the CALC section of the STAT menu. The screen display shows that the
relation

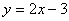
fits the data.

Just to recap:

For any linear function, the first difference in a finite difference table is always constant. This constant is the gradient of the linear function and the y-intercept is given by y(0).

Find a rule for the function specified by the following tables; and check your answers with a graphics calculator.

c.

d.

e.

f.

g.

h.

i.

j.

k.

l.

m.

n.

o.