A quadrilateral is a closed plane figure bounded by four line
segments. For example, the figure ABCD shown here is a
quadrilateral.
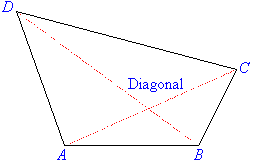
A line segment drawn from one vertex of a quadrilateral to the opposite
vertex is called a diagonal of the quadrilateral. For example, AC is a diagonal of quadrilateral ABCD, and so is BD.
Types of Quadrilaterals and their Properties
There are six basic types of quadrilaterals:
1. Rectangle
- Opposite sides are parallel and equal.
- All angles are 90º.
- The diagonals bisect each other.

2. Square
- Opposite sides are parallel and all sides are equal.
- All angles are 90º.
- Diagonals bisect each other at right angles.

3. Parallelogram
- Opposite sides are parallel and equal.
- Opposite angles are equal.
- Diagonals bisect each other.

4. Rhombus
- All sides are equal and opposite sides are parallel.
- Opposite angles are equal.
- The diagonals bisect each other at right angles.

5. Trapezium
- A trapezium has one pair of opposite sides parallel.
- A regular trapezium has non-parallel sides equal and its base angles
are equal, as shown in the following diagram.

6. Kite
- Two pairs of adjacent sides are equal.
- One pair of opposite angles is equal.
- Diagonals intersect at right angles.
- The longest diagonal bisects the shortest diagonal into two equal
parts.

Theorem 3
Prove that the angle sum of a quadrilateral is equal to 360º.
Proof:


Hence the angle sum of a quadrilateral is 360º.
Applying Properties of Angles in Quadrilaterals
The theorems we have proved can be used to prove other theorems. They
can also be used to find the values of the pronumerals in a problem.
Example 14
Find the value of the pronumeral x in the accompanying diagram.
Give reasons for your answer.

Solution:

Example 15
Find the value of each of the pronumerals in the kite shown here. Give reasons
for your answers.

Solution:


Example 16
Find the value of each of the pronumerals in the accompanying diagram. Give
reasons for your answers.

Solution:


Example 17
Find the value of the pronumeral in the accompanying diagram. Give
reasons for your answer.

Solution:

Example 18
Find the value of each of the pronumerals in the accompanying diagram. Give
reasons for your answers.

Solution:


Example 19
Find the value of the pronumeral in the accompanying diagram. Give
reasons for your answer.

Solution:




Key Terms
quadrilateral, diagonal of a
quadrilateral, rectangle, square, parallelogram, rhombus, trapezium, regular trapezium, kite, angle sum of a quadrilateral |