In this section we will consider arcs, subtended
angles, the angle at the circumference and the Angle at
Centre Theorem.
Arcs
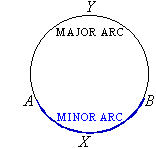
An arc is a curved line along the circumference of a circle.
For example, AXB is a minor arc, and AYB is a major
arc.
Subtended Angles
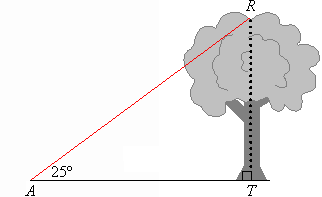
The angle RAT is said to be the angle subtended by the tree TR at A. So, the tree subtends an angle of 25º at A.
This can be described as follows.
'An angle of 25º is subtended at A by the tree'.
Angle at the Circumference
If the end points of an arc are joined to a third point on the
circumference of a circle, then an angle is formed.
For example, the minor arc AB subtends an angle of 45º at C.
The angle ACB is said to be the angle subtended by the minor arc AB (or simply arc AB) at C.
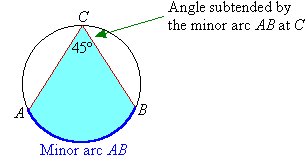
The angle ACB is an angle at the circumference standing on the
arc AB.
Angle at the Centre
If the end points of an arc are joined to the centre of a circle, then
an angle is formed. For example, the minor arc AB subtends an
angle of 105º at O. The angle AOB is said to be the
angle subtended by the minor arc AB (or simply arc AB) at
the centre O.
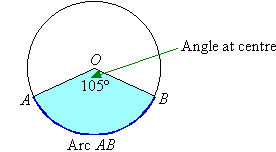
The angle AOB is an angle at the centre O standing on the
arc AB.
Angle at Centre Theorem
Theorem
Use the information given in the diagram to prove that the angle at the
centre of a circle is twice the angle at the circumference if both angles
stand on the same arc.
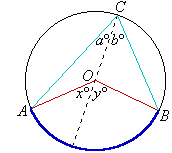
Given:
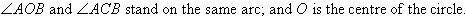
To prove:
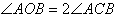
Proof:
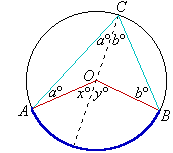
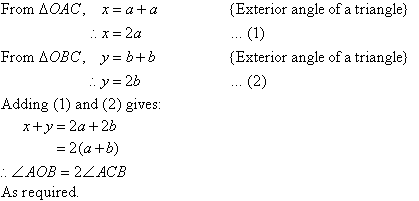
In general:
The angle at the centre of a circle is twice the angle at the
circumference if both angles stand on the same arc. This is called the Angle
at Centre Theorem.
We also call this the basic property, as the other angle
properties of a circle can be derived from it.
Example 22
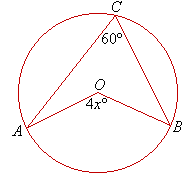
Find the value of the pronumeral in the following circle centred at O.
Solution:
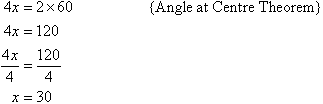
Example 23
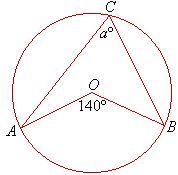
Find the value of the pronumeral in the following circle centred at O.
Solution:
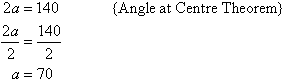
Angle in a Semi-Circle
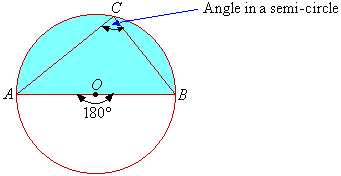

In general:
The angle in a semi-circle is a right angle.
Example 24
Find the value of the pronumeral in the following circle centred at O.
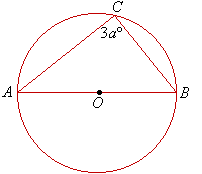
Solution:

Key Terms
arc, minor arc, major
arc, subtended angle, angle at the circumference, angle at the centre, Angle
at Centre Theorem, basic property of a circle, angle in a
semi-circle |