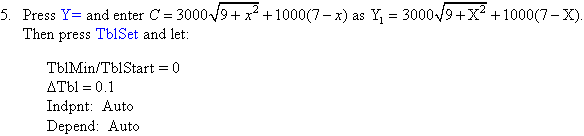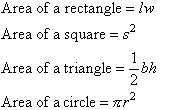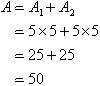Project 13.1 Squares and Square Roots
Formulas containing squares and square roots often occur in science. To
perform numerical computations we need to find rational numbers that
approximate the value of the squares and/or square roots.




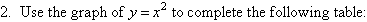

Extension
3.
a. Use a ruler and protractor to draw a right-angled triangle ABC having AB = 2 cm,
BC = 1.5 cm and angle ABC = 90º.
b. Use a ruler to find the length of the hypotenuse of the
right-angled triangle.
c. Verify your answer by finding the length of the hypotenuse using
Pythagoras' Theorem.
Project 13.2 Minimum Cost
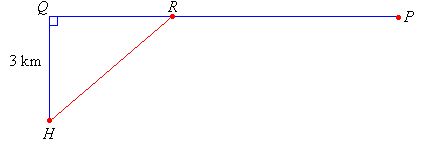
In the accompanying diagram, a hotel is situated 3 km from a highway.
The owner of the hotel is thinking of connecting to a gas supply for
heating and cooking purposes. At present the nearest gas pipe stops 7 km
down the highway.
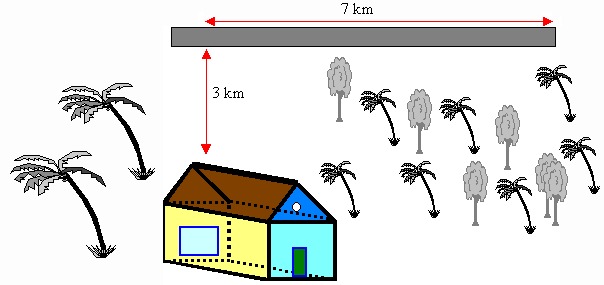
The cost of extending the gas pipe through the bush is three times as
much as the cost of extending the pipe along the highway. How should the
gas pipe be placed to minimise the cost of connecting it to the hotel?
To investigate the cost of laying the gas pipe to the hotel, you may
proceed as follows:
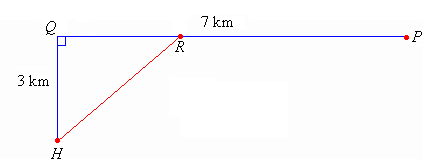
1. Draw a graphical model (as displayed below) from the
information given above.

2. The gas pipe is laid from P to R and then from R to H. If QR = x km, express the following in terms of x:
a. the length of PR
b. the length of HR
3. If the cost of extending the gas pipe along the highway is
$1000 per kilometre, find:
a. the cost of extending the gas pipe along the highway
b. the cost of extending the gas pipe from the highway to the
hotel.
4. Let the total cost of extending the gas pipe from P to R and from R to H be $C. Show that C is given by
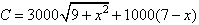
Modelling with a TI-82/83 Graphics Calculator
A graphics calculator can be used to determine the minimum and/or
maximum values of a function. In this project, you are required to find
the minimum cost of extending the gas pipe to the hotel. You may proceed
as follows:
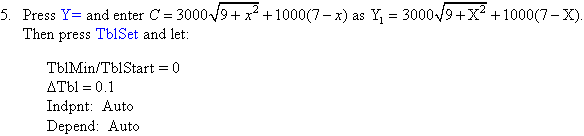
To create a table of values of Y1 (i.e. C) for
different values of x, press Table.
Using this table determine:
a. the value of x which gives the minimum value of C
b. the minimum cost of extending the gas pipe.
6. Use trigonometry to find the angle QRH.
7. Display the measurements for the lengths of PR, QR, HR and the angle QRH in the following diagram.
Modelling with Excel
Microsoft® Excel spreadsheets can be used quite effectively to
generate a table of values. In this project, you are required to find the
minimum cost of extending the gas pipe. You may proceed as follows:
- Open a new spreadsheet, and type x in the cell A1 and C in the cell B1.
- Type 0 in the cell A2. Then type the formula = A2 + 0.05 into the
cell A3 and fill down (using the edit fill down command) this formula
to an appropriate row.
- Type the formula for the cost C in the cell B2 and fill down
the formula to an appropriate row.
8. Using the values generated in the spreadsheet determine:
a. the value of x which gives the minimum value of C
b. the minimum cost of extending the gas pipe.
9. Use trigonometry to find the angle QRH.
10. Display the measurements for the lengths of PR, QR, RH and the angle QRH in the following diagram.

Write a brief report on your findings by comparing the results obtained
from the two different methods.
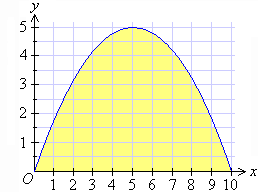
Project 13.3 Area under the Curve
We know that:
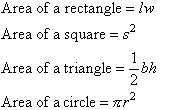
In this project, you are required to determine the area that is above
the x-axis and under the parabola
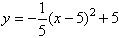

We do not know a formula that can be used to find the shaded area.
However, we can find an approximate value of the shaded area enclosed
under the curve and above the x-axis by dividing it into small
regions, say rectangles, as shown below.
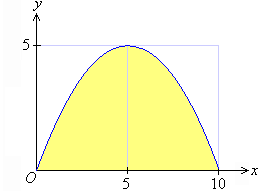
It is clear from the diagram that the area under the curve and above
the x-axis is approximately equal to the sum of the two rectangles.
That is:
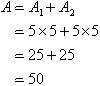
So, the shaded area is approximately 50 square units.
In the above example, the width of each rectangle is 5 units. This is
known as the strip width.
We can obtain a better approximation to the area under the curve of a
function by increasing the number of rectangles (i.e. strips). Reducing
the width of the rectangles (i.e. strips) increases the number of
rectangles.
1. Determine the area under the curve
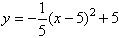
and above the x-axis by dividing the area into rectangles of
width 2 units. That is, divide the shaded area into 5 rectangles.

2. Determine the area under the curve
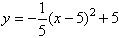
and above the x-axis by dividing the area into rectangles of
width 1 unit. That is, divide the shaded area into 10 rectangles.
For questions 3, 4, 5 and 6 use Excel and/or a graphics calculator.
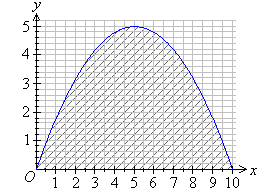
3. Determine the area under the curve
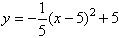
and above the x-axis by dividing the area into rectangles of
width 0.5 units.
4. Determine the area under the curve
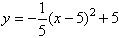
and above the x-axis by dividing the area into rectangles of
width 0.4 units.

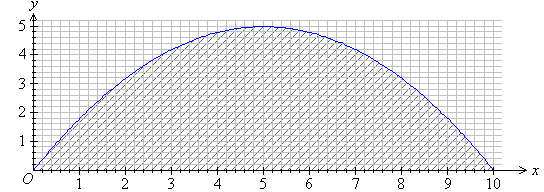
5. Determine the area under the curve
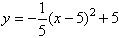
and above the x-axis by dividing the area into rectangles of
width 0.2 units.
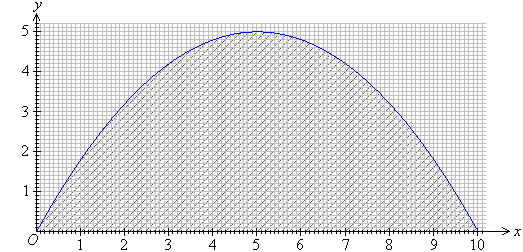
6. Determine the area under the curve
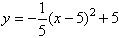
and above the x-axis by dividing the area into rectangles of
width 0.1.
|