Project 15.1 Table of Sine Values
Draw the unit circle shown, and divide the radius into 10 equal parts
so that each part represents 0.1.
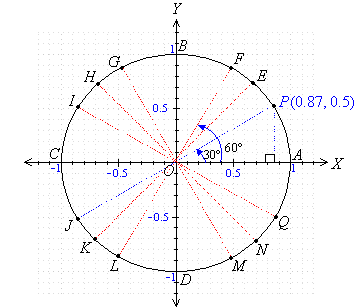
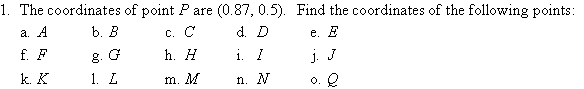
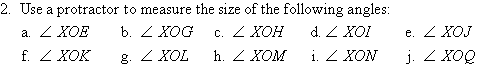

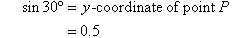
3. Use a ruler and protractor to create a table of sine values
correct to one decimal place.
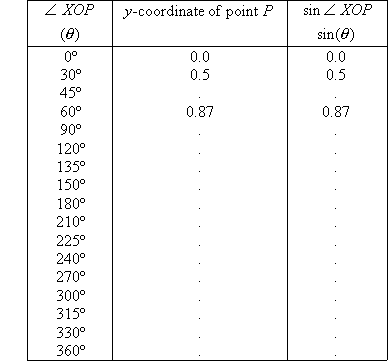

6. If a plane is divided into four equal parts by a set of axes,
then each part is called a quadrant.
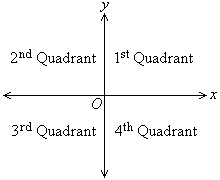
In the first quadrant, the angle is between 0º and 90º.
In the second quadrant, the angle is between 90º and 180º.
In the third quadrant, the angle is between 180º and 270º.
In the fourth quadrant, the angle is between 270º and 360º.
We observe from the unit circle and question 3 that the
value of sine of an angle in the first quadrant is + (i.e. positive). What
is the sign (i.e. positive or negative) of the sine of an angle in the:
a. second quadrant.
b. third quadrant.
c. fourth quadrant.
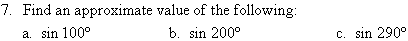
Your report should include the following:
- A statement of the project in your own words
- The tables, graphs and all working
- References
- Acknowledgments
- Appendices
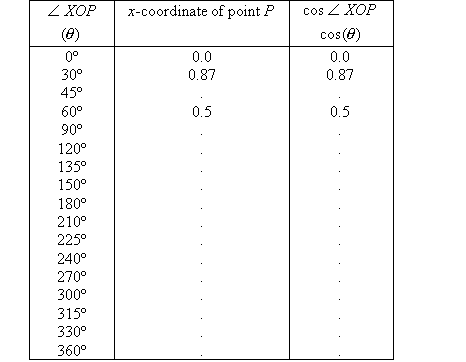
Project 15.2 Table of Cosine Values
Draw the unit circle shown, and divide the radius into 10 equal parts
so that each part represents 0.1.


1. Use a ruler and protractor to create a table of cosine values
correct to one decimal place.
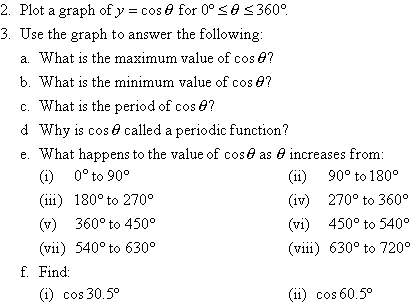
4. If a plane is divided into four equal parts by a set of axes, then
each part is called a quadrant.

In the first quadrant, the angle is between 0º and 90º.
In the second quadrant, the angle is between 90º and 180º.
In the third quadrant, the angle is between 180º and 270º.
In the fourth quadrant, the angle is between 270º and 360º.
We observe from the unit circle and question 1 that the
value of cosine of an angle in the first quadrant is + (i.e. positive).
What is the sign (i.e. positive or negative) of the cosine of an angle in
the:
a. second quadrant.
b. third quadrant.
c. fourth quadrant.
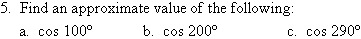
Your report should include the following:
- The statement of the project in your own words
- The tables, graphs and all working
- References
- Acknowledgments
- Appendices
Project 15.3 Table of Tangent Values
Draw the unit circle shown, and divide the radius into 10 equal parts
so that each part represents 0.1.

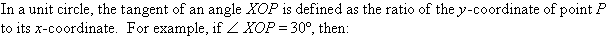
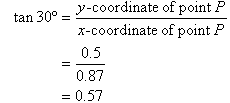
1. Use a ruler and protractor to create a table of tangent values
correct to one decimal place.
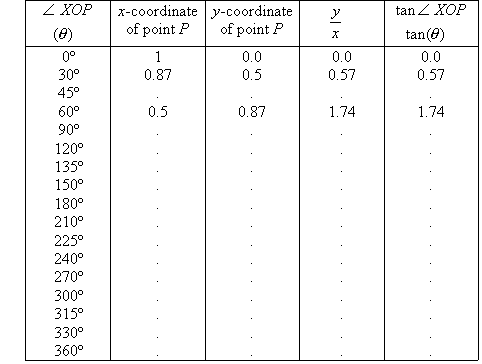

4. If a plane is divided into four equal parts by a set of axes, then
each part is called a quadrant.

In the first quadrant, the angle is between 0º and 90º.
In the second quadrant, the angle is between 90º and 180º.
In the third quadrant, the angle is between 180º and 270º.
In the fourth quadrant, the angle is between 270º and 360º.
We observe from the unit circle and question 1 that the
value of the tangent of an angle in the first quadrant is + (i.e.
positive). What is the sign (i.e. positive or negative) of the tangent of
an angle in the:
a. second quadrant.
b. third quadrant.
c. fourth quadrant.
Your report should include the following:
- The statement of the project in your own words
- The tables, graphs and all working
- References
- Acknowledgments
- Appendices
|