| An experiment was conducted involving a cyclist, runner,
jogger and walker each completing a journey of 40 km. The results of the
experiment are recorded in the table shown below.
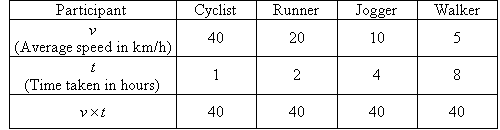
The values recorded in the table show some interesting facts:
- As the average speed increases, the time taken to complete the
journey decreases.
- An increase in one variable causes a decrease in the other.
- Neither variable can be equal to 0.
- The product of two variables has a constant value (i.e. vt =
40).
- The value of v decreases as the value of t increases.
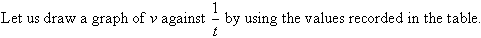

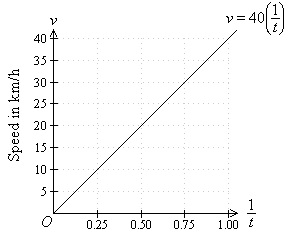

In such a case, we say that:
- v varies inversely as t; or
- v is inversely proportional to t; or
- v varies directly as the reciprocal of t.
This is written as:
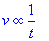
In the example under discussion,
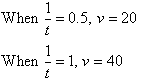
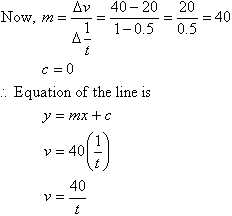
In general:
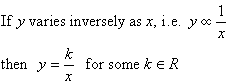
The constant k is called the constant of variation or the constant of proportionality.
Some practical examples of inverse variation are given below.
1. The pressure, P, of a given mass of a gas in a closed
cylinder varies inversely as the volume, V, of the cylinder. That
is:
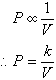
2. The current, I amps, produced by a battery is inversely
proportional to the resistance, R ohms, of the circuit that the
battery is connected to. That is:
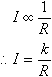
Example 14
If y varies inversely as x, and x = 3 when y = 4, find y when x = 8.
Solution:

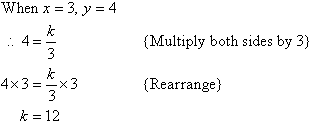
Substituting k = 12 in (1) gives:

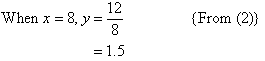
Note:
- Inverse variation exists if the value of one variable decreases as
the value of the other variable increases.
For example, as the speed of the vehicle increases, the time taken to
complete the journey decreases.
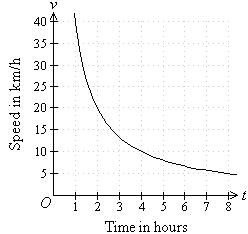
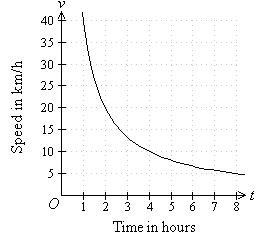
- Graphical representation of inverse variation takes the shape of a
hyperbola, as shown above.
Key Terms
inverse variation |