
We know that the decimal numbers increase in size as we move to the right
on the number line.
For example, 0.4 is less than 0.7.
Let us now compare 1.57 and 1.6.
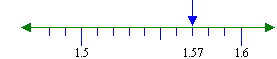
From the number line, we notice that 1.57 is less than 1.6. This
suggests that:
To compare two decimal numbers, compare digits in corresponding positions
from left to right until the larger number is identified.
In the above example, the units digit is 1 for both numbers and the
tenths digit is 5 and 6 for the respective numbers.
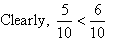
So, 1.57 is less than 1.6.
Thus, 1.6 is the larger number.
Example 6
Find the larger number in each pair:
a. 3.6 and 3.63
b. 5.738 and 5.74
c. 29.86527 and 29.869613
Solution:
a. 3.6 is the same as 3.60. Now to compare 3.60 and 3.63,
compare the digits in corresponding positions from left to right until the
larger number is identified.
The units digit is 3 and the tenths digit is 6 for both numbers.
The hundredths digit is 0 and 3 for the respective numbers.
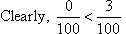
So, 3.6 is less than 3.63.
Thus, 3.63 is the larger number.
b. 5.74 is the same as 5.740. Now to compare 5.738 and 5.740,
compare the digits in corresponding positions from left to right.
The units digit is 5 and the tenths digit is 7 for both numbers.
The hundredths digit is 3 and 4 for the respective numbers.
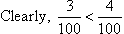
So, 5.738 is less than 5.74.
Thus, 5.74 is the larger number.
c. To compare 29.86527 and 29.869613, compare the digits in
corresponding positions from left to right.
The tens digit, units digit, tenths digit and hundredths digit are the
same for both numbers. The thousandths digit is 5 and 9 for the
respective numbers.
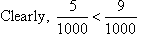
So, 29.86527 is less than 29.869613.
Thus, 29.869613 is the larger number.
|