| Consider a rectangle of length l cm and width w cm.
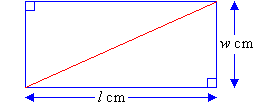
Draw a diagonal and cut out the rectangle. Then cut along the
diagonal to form two right-angled triangles.
By arranging one triangle over the other, we find that the triangles are congruent. In other words, the triangles are the same size and thus,
equal in area. This suggests that the area of a triangle is equal to
half the area of a rectangle around it. Therefore:
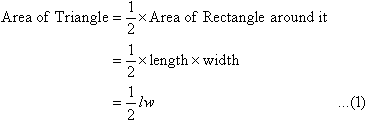
In the diagram, we notice that the length of the rectangle is one side of
the triangle. This is said to be the base of the
triangle. So:
Base of the triangle = Length of the rectangle
The distance from the top of the triangle to the base is called the height of the triangle. Therefore:
Height of the triangle = Width of the rectangle

Replacing l and w with the Base and Height in equation (1), we obtain:
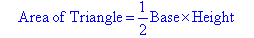
Using the pronumerals A for area, b for base and h for height, we can
write the formula for the area of a right-angled triangle as:
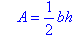
Area of a Triangle
Consider the following triangle.
Enclose the triangle by drawing a rectangle around it as shown below.
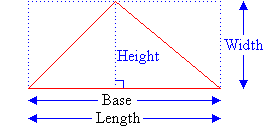
It is clear from the diagram that the length of the rectangle is one side
of the triangle. This is said to be the base of the
triangle. So:
Base of the triangle = Length of the rectangle
The distance from the top of the triangle to the base is called the
height of the triangle. Clearly:
Height of the triangle = Width of the rectangle
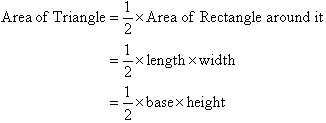
Using the pronumerals A for area, b for base and h for height, we can
write the formula for the area of a triangle as:
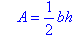
Note:
The rule (or equation)
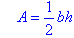
represents the relationship between the base and height of a triangle and its area.
Such an equation, which gives a rule for working out the value of one
quantity from the values of others is called a formula.
Just to recap the ongoing discussion:
|