Recall that:
An equation is a statement that contains an equal sign.
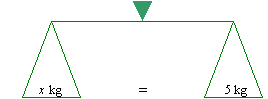
Consider the simple equation
x = 5
Visualise this equation as a balanced pair of scales with x and 5
measured in kilograms.
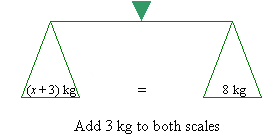
If we add 3 kg to the scale on the left-hand side, the scales will
balance as long as we add 3 kg to the scale on the right-hand side.
That is, x + 3 = 8.
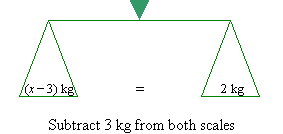
Also, if we subtract the same weight, say 3 kg, from each side of the
balance, the scales will remain balanced. That is, x – 3 = 2.
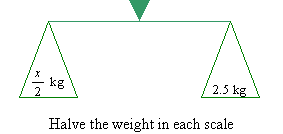
If we double the weight in the scale on the left-hand side, the scales
will balance as long as we double the weight in the scale on the right-hand
side. That is, 2x = 10.
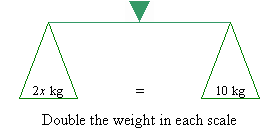
Also, if we halve the weight in each scale of the balance, the scales
will remain balanced.
Solving Equations
Solving an equation means to find the value of a pronumeral that
makes a statement true.
In the preceding section, we observed that:
An equation behaves like a pair of balanced scales. The scales
remain balanced as long as we do the same thing to both scales.
This suggests that to solve an equation, we can do the same thing to both
sides of an equation. That is:
- The same number can be subtracted from both sides of an
equation.
- The same number can be added to both sides of an equation.
- Both sides of an equation can be divided by the same number.
- Both sides of an equation can be multiplied by the same number.
We will now consider equations involving addition, subtraction,
multiplication and division.
Operations such as +, –, × and ÷ are used to
build an equation. To solve an equation, we use inverse (i.e.
opposite) operations such that the pronumeral is the only term remaining on
the left-hand side.
Equations Involving Addition
The inverse operation of + is –. So, to solve an equation involving addition, we undo the addition by subtracting the same number from
both sides.
Example 3
Solve the equation x + 6 = 14.
Solution:
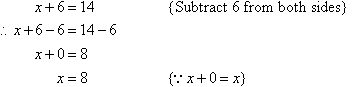
Note:
6 is added to x. So, we undo the addition by subtracting 6
from both sides.
Check:
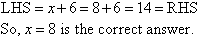
Equations Involving Subtraction
The inverse operation of – is +. So, to solve an equation involving subtraction, we undo the subtraction by adding the same number to
both sides.
Example 4
Solve the equation x – 9 = 17.
Solution:
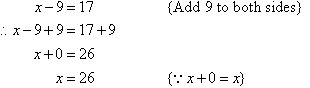
Note:
9 is subtracted from x. So, we undo the subtraction by
adding 9 to both sides.
Check:
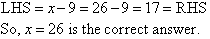
Equations Involving Multiplication
The inverse operation of × is ÷. So, to solve an equation involving multiplication, we divide both sides of the equation by the same
number.
Example 5
Solve the equation 8x = 72.
Solution:

Note:
x is multiplied by 8. So, we undo the multiplication by
dividing both sides by 8.
Check:
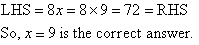
Equations Involving Division
The inverse operation of ÷ is ×. So, to solve an equation involving division, we multiply both sides of the equation by the same
number.
Example 6
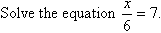
Solution:
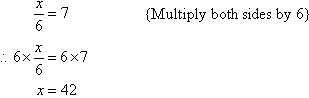
Note:
x is divided by 6. So, we undo the division by multiplying both
sides by 6.
Check:
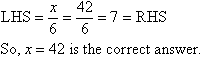
Remember:
- An equation is a statement that contains an equal sign.
- To solve an equation, we do the same thing to both sides of the equation.
- The same number can be subtracted from both sides of an equation.
- The same number can be added to both sides of an equation.
- Both sides of an equation can be divided by the same number.
- Both sides of an equation can be multiplied by the same number.
Key Terms
solving an equation |