Problem 15.1 Modelling the Number of Sleepers
Sleepers can be used to divide a garden into separate beds as shown in
the following diagrams:

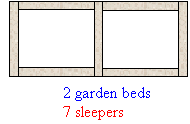
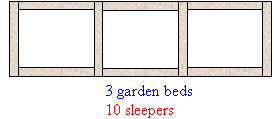
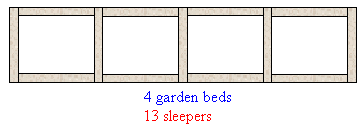
1. One garden bed requires 4 sleepers, two garden beds require 7
sleepers, three garden beds require 10 sleepers and four garden beds require
13 sleepers.
a. How many sleepers are required for 5 garden beds?
b. How many sleepers are required for 6 garden beds?
c. How many sleepers are required for 7 garden beds?
2. Let b represent the number of garden beds and s the
number of sleepers.
a. Complete the following table:

b. In mathematics, patterns in numbers are often used to discover a rule for
finding the next number. When we look for a pattern in numbers, we try to
look at each number and find out how it relates to other numbers. This
enables us to state a rule in words and then write it algebraically. By observing the pattern in the above table, find the relationship
that exists between b and s.
3. Draw a graph of s against b.
4. How many pieces of sleepers would be needed for 100 garden beds?
5. How many pieces of sleepers would be needed for 1000 garden beds?
Problem 15.2 Modelling the Number of Chairs
Chairs can be arranged to surround tables as shown in the following
diagrams:
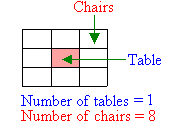
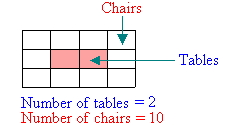
1. From the diagrams above, we notice that 8 chairs can surround one table
and 10 chairs can surround two tables. Draw a similar diagram to work out
how many chairs can be arranged to surround 3 tables?
2. Let t represent the number of tables and c the number of
chairs. Complete the following table.
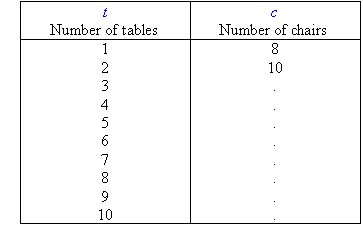
3. In mathematics, patterns in numbers are often used to discover a rule for
finding the next number. When we look for a pattern in numbers, we try to
look at each number and find out how it is related to other numbers. This
enables us to state a rule in words and then write it algebraically. By observing the pattern in the above table, find the
relationship that exists between t and c.
4. Draw a graph of c against t.
5. How many chairs can be arranged to surround 15 tables?
6. How many chairs can be arranged to surround 20 tables?
|