|
A directional compass is shown below. It is used to find a
direction or bearing .
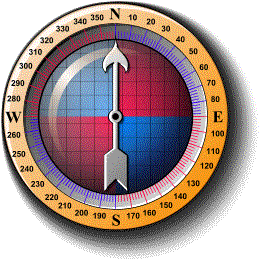
The four main directions of a compass are known as cardinal points.
They are north (N), east (E), south (S) and west (W). Sometimes, the
half-cardinal points of north-east (NE), north-west (NW), south-east (SE)
and south-west (SW) are shown on the compass. The above compass shows
degree measurements from 0° to 360° in 10° intervals with:
- north representing 0° or 360°
- east representing 90°
- south representing 180°
- west representing 270°
When using a directional compass, hold the compass so that the point
marked north points directly away from you. Note that the magnetic
needle always points to the north.
Bearing
The true bearing to a point is the angle measured in
degrees in a
clockwise direction from the north line. We will refer to the true
bearing simply as the bearing.
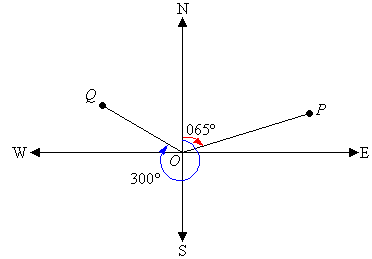
For example, the bearing of point P is 065º which is the number
of degrees in the angle measured in a
clockwise direction from the north line to the line joining the
centre of the compass at O with the point P (i.e. OP).
The bearing of point Q is 300º which is the number of degrees in
the angle measured in a
clockwise direction from the north line to the line joining the centre of the
compass at O with the point Q (i.e. OQ).
Note:
The bearing of a point is the number of degrees in the angle measured in a
clockwise direction from the
north line to the line joining the centre of the compass with the point.
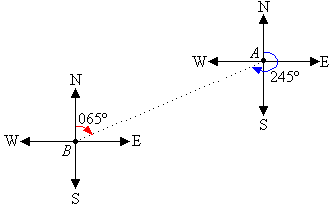
A bearing is used to represent the direction of one point relative to
another point.
For example, the bearing of A from B is 065º. The
bearing of B from A is 245º.
Note:
- Three figures are used to give bearings.
- All bearings are measured in a horizontal plane.
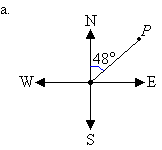
Example 10
State the bearing of the point P in each of the following diagrams:
Solution:
a. Mark the angle in a
clockwise direction by indicating the turn between the north line and
the line joining the centre of the compass to the point P.
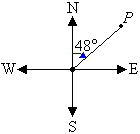
The bearing of point P is 048°.
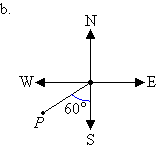
b. Mark the angle in a
clockwise direction by indicating the turn between the north line and
the line joining the centre of the compass to the point P.
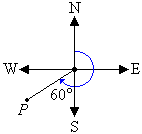
The cardinal point S corresponds to 180°. It is clear from the
diagram that the required angle is 60° larger than 180°. So, the
angle measured in a
clockwise direction from the north line to the line joining the centre of the compass
to point P is 180° + 60° = 240°.
So, the bearing of point P is 240°.
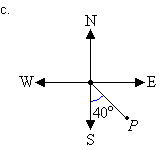
c. Mark the angle in a
clockwise direction by indicating the turn between the north line and
the line joining the centre of the compass to the point P.
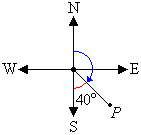
The cardinal point S corresponds to 180°. It is clear from the
diagram that the required angle is 40° less than 180°. So, the angle measured in a
clockwise direction from the north line to the line joining the centre of the compass to
point P is 180° – 40° = 140°.
So, the bearing of point P is 140°.
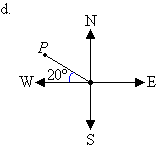
d. Mark the angle in a
clockwise direction by indicating the turn between the north line and
the line joining the centre of the compass to the point P.
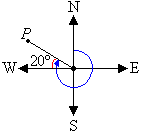
The cardinal point W corresponds to 270°. It is clear from the
diagram that the required angle is 20° larger than 270°. So, the
angle measured in a
clockwise direction from the north line to the line joining the centre of the compass
to point P is 270° + 20° = 290°.
So, the bearing of point P is 290°.
Direction
The conventional bearing of a point is stated as the number of
degrees east or west of the north-south line. We will refer to the
conventional bearing simply as the direction.
To state the direction of a point, write:
- N or S which is determined by the angle
being measured
- the angle between the north or south line and the point,
measured in degrees
- E or W which is determined by the location of the point
relative to the north-south line
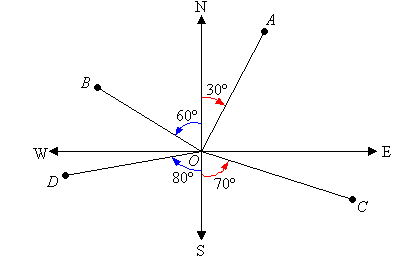
E.g. In the above diagram, the direction of:
- A from O is N30ºE.
- B from O is N60ºW.
- C from O is S70ºE.
- D from O is S80ºW.
Note:
N30ºE means the direction is 30º east of north.
Example 11
Describe each of the following bearings as directions.
a. 076°
b. 150°
c. 225°
d. 290°
Solution:
a. The position of a point P on a bearing of 076° is shown in the
following diagram.
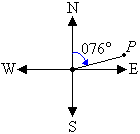
The position of the point P is 76° east of north. So, the
direction is N76°E.
b. The position of a point P on a bearing of 150° is shown in the
following diagram.
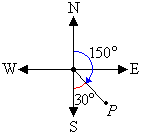
The position of the point P is 180° – 150° = 30° east
of south. So, the direction is S30°E.
c. The position of a point P on a bearing of 225° is shown in the
following diagram.
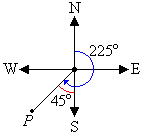
The position of the point P is 225° – 180° = 45° west
of south. So, the direction is S45°W.
d. The position of a point P on a bearing of 290° is shown in the
following diagram.
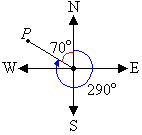
The position of the point P is 360° – 290° = 70° west
of north. So, the direction is N70°W.
Key Terms
directional compass, cardinal
points, true bearing, bearing,
direction, conventional bearing
|